Introduzione al concetto di variabile e al calcolo letterale
Le attività sono state progettate sotto forma di Moduli Google con la correzione di alcune risposte attraverso spiegazioni aggiuntive presentate in forma scritta o sotto forma di video, in modo da permettere il lavoro autonomo degli studenti. Gli insegnanti che le stanno utilizzando fanno seguire un momento di condivisione e sintesi in videoconferenza.
Il link “Visualizza” permette di vedere una versione di esempio dell’attività.
Il link “copia” permette di copiare il Modulo Google nel proprio Drive, in modo da gestire autonomamente il questionario e le risposte dei propri studenti.
L’obiettivo delle attività che seguono è quello di introdurre la variabile e il calcolo letterale per generalizzare situazioni che presentano una sequenza di costruzioni in cui è utile cercare le regolarità*. Alcuni insegnanti le stanno utilizzando nella classe terza.
|
|
Visualizza |
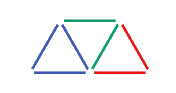
Nella prima attività si richiede la generalizzazione della costruzione proposta, dopo aver studiato alcuni casi particolari. In conclusione due video mostrano come si arriva all’introduzione della variabile e confrontano due procedimenti diversi. |
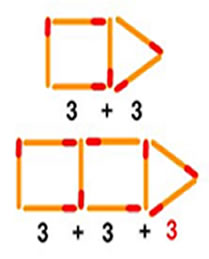 |
La seconda attività, simile alla prima, può essere utilizzata per verificare la comprensione del processo di generalizzazione. | |
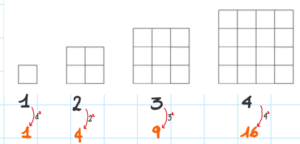 |
Nella terza attività si lavora sul quadrato di un numero (adatta anche per la seconda SSPG). In questo modulo la correzione avviene a lavoro svolto, cliccando su “Visualizza se la risposta è corretta“. | |
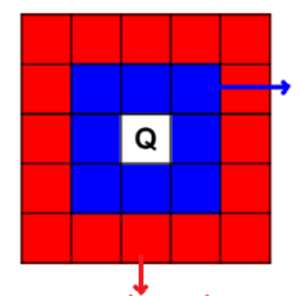 |
La quarta attività è stata pensata come attività di potenziamento. | |
|
L’obiettivo delle attività che seguono è quello di scoprire la proprietà distributiva applicata al calcolo letterale, partendo dall’ambito geometrico. L’area di un rettangolo viene descritta attraverso diverse scomposizioni a cui corrispondono le rispettive espressioni letterali e la loro equivalenza viene ricostruita anche attraverso la manipolazione algebrica che fa riferimento a proprietà opportune. |
||
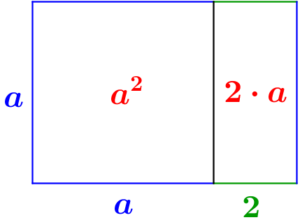 |
Attività introduttiva per arrivare a gestire il prodotto a·(a+2) | |
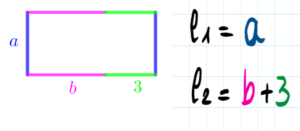 |
Attività intermedia relativa al prodotto a·(b+3) |
|
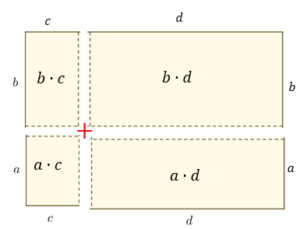 |
Attività conclusiva per manipolare il prodotto (a+b )·(c+d) |
|
Progettato dal laboratorio DiCoMat dell’Università degli Studi di Trento in collaborazione con Letizia Corazzolla, Veronica Gasparin, Chiara Micheloni, Elisabetta Ossanna, Stefano Pegoretti e Carlotta Vielmo.
*I problemi proposti per la ricerca di regolarità prendono spunto principalmente da quesiti Invalsi (www.gestinv.it).