In questa pagina viene descritta un’attività laboratoriale sulle reti minime per la scuola secondaria di primo grado che ripropone, con delle modifiche, l’attività descritta nel libro – Problemi di massimo e di minimo – Quaderni di laboratorio di Domenico Luminati e Italo Tamanini- Edizioni Mimesis 2009.
LA METODOLOGIA
L’attività riportata su questa pagina è laboratoriale di tipo manipolativo, da svolgersi con l’utilizzo di schede guidate, in gruppi di lavoro, il più omogenei possibile, composti da 4-5 studenti. Sono inoltre state pensate in modo tale da favorire la scrittura con l’obbiettivo di sviluppare nel ragazzo un adeguato linguaggio matematico. Viene fatto un ampio uso di artefatti e nella sperimentazione di tali laboratori si è cercato di favorire la discussione matematica riducendo al minimo gli interventi frontali. Si è cercato anche di sviluppare gli argomenti tenendo conto di una loro articolazione in un curricolo verticale.
L’ATTIVITÀ
Durata minima: 4 ore
La durata del laboratorio che viene indicata è da intendersi come una stima dato che dipenderà dall’insegnante scegliere se e quali punti dell’attività approfondire. Inoltre il tempo di esecuzione dipende da molti altri fattori tra i quali il livello della classe, l’ambiente di lavoro che si instaura e l’orario scolastico di cui si dispone
Collocazione nel curricolo
Questo laboratorio è rivolto alle classi terze delle scuole secondarie di primo grado e al primo biennio delle scuole secondarie di secondo grado
Obbiettivi
Studiare le reti minime che collegano dei punti del piano, lavorare con le figure geometriche piane quali il triangolo e il quadrato e applicare le loro proprietà, confrontare numeri, lavorare con i numeri irrazionali. Oltre agli obbiettivi già elencati si vogliono perseguire anche i seguenti obbiettivi trasversali: stimolare la collaborazione e la condivisione del sapere, esercitarsi nella misura di oggetti, sviluppare un linguaggio matematico appropriato e abituare i ragazzi a comunicare i loro procedimenti risolutivi.
Descrizione
FASE 1: TRIANGOLO EQUILATERO
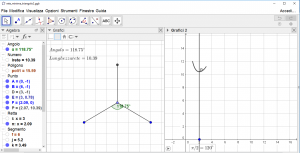
I ragazzi, con della corda, devono collegare i tre occhioli di un modellino di compensato che rappresentano tre città poste ai vertici di un triangolo equilatero, cercando di rendere il percorso il più breve possibile. Una volta fatta la loro ipotesi, cioè trovata quella che secondo loro è la rete minima, la verificano utilizzando le lamine di sapone. Infine, con una discussione mediata e con l’utilizzo di un file geogebra, viene data una dimostrazione intuitiva del fatto che la rete minima è quella disegnata dalla lamina di sapone.
FASE 2: TRIANGOLO RETTANGOLO
Questa fase vede i ragazzi impegnati nel ricercare la rete minima che collega tre punti posti ai vertici di un triangolo rettangolo. Anche in questo caso utilizzano prima il modellino di compensato e poi le lamine di sapone.
FASE 3: QUADRATO
L’ultima fase dell’attività vede i ragazzi impegnati nella ricerca della rete minima che collega quattro città poste ai vertici di un quadrato. Sempre utilizzando il modellino in compensato e della corda cercano, andando per tentativi, il percorso più breve. Infine verificano il risultato con le lamine di sapone e, con una discussione mediata, utilizzando i numeri irrazionali verificano che la lunghezza del percorso trovato è minore di quella degli altri.
Nota: nel box download è presente una descrizione più dettagliata del laboratorio
Materiali
- schede guida per lo studente fornite dall’insegnante presenti nel box download (una copia per ragazzo)
- Modellino di compensato 60 cm* 60 cm con occhioli ai vertici di un triangolo equilatero e di un quadrato
- Corda: circa 20 metri per gruppo di lavoro
- 1 bacinella per gruppo di lavoro
- 1 lastrina trasparente con 3 perni a triangolo equilatero per gruppo di lavoro
- 1 lastrina trasparente con 4 perni a quadrato per gruppo di lavoro
- 1 lastrina trasparente con 4 perni a “T” per gruppo di lavoro
- 1 righello plastificato per gruppo di lavoro
- 2 indicatori di angoli a per gruppo di lavoro
- 1 serie di 4 tessere sulle possibili reti del triangolo equilatero (gialle) per gruppo di lavoro
- 1 serie di 9 tessere sulle possibili reti del quadrato (rosse) per gruppo di lavoro
- 1 lastrina trasparente con 5 perni a pentagono
- 1 lastrina trasparente con 6 perni ad esagono
- Telai per bolle a cerchio, quadrato e cuore
- File geogebra per la rete minima del triangolo equilatero (presente nel box download)
- Stecca da 50 cm, squadre, matite, post-it e cancelleria varia
|
DOWNLOAD Descrizione del laboratorio: Laboratorio Schede guida per lo studente: Schede Link al file geogebra: https://www.geogebra.org/worksheet/edit/id/Rgnwk38p |