| Modalità d’uso per il docente
Ora disponiamo di vari strumenti relativi alla variabile aleatoria normale, dunque possiamo comprendere più a fondo il risultato di approssimazione introdotto all’inizio del percorso. In particolare, le prime due attività consentono, mediante un approccio operativo-sperimentale, di dedurre e apprezzare l’enunciato semplificato del teorema limite centrale. Le attività si prestano ad essere svolte individualmente e si avvalgono di file Geogebra. Al docente spetterà poi raccogliere le considerazioni fatte e discutere le conclusioni con gli studenti. Per enunciare la sostanza del teorema, invece, è presente una dispensa, pensata a supporto di una lezione condotta in modalità partecipata. Seguono due applicazioni che gli studenti dovrebbero ormai essere in grado di risolvere individualmente. Ad esse andrebbero poi aggiunti altri esercizi di consolidamento, desunti magari dal libro di testo e/o da prove dell’esame di Stato. |
1. esplorazioni: i parametri -attivita’-
Riassumendo…
La nostra investigazione sull’approssimazione della binomiale inizia dall’esame dei valori da attribuire ai parametri della variabile aleatoria normale. Si tratta di un’attività di scoperta che lo studente può svolgere tramite il file Geogebra proposto.

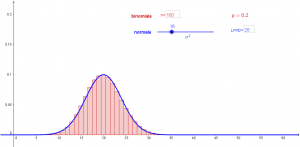
Link al file Geogebra: parametri
Link al file: attività1
2. esplorazioni: il numero di prove -attivita’-
Riassumendo…
Fissato il legame tra i parametri della distribuzione normale e quelli della binomiale, è interessante sondare la convergenza, ossia studiare cosa succede al crescere del numero di prove dello schema di Bernoulli. Anche in questa attività è presente un file Geogebra mediante il quale lo studente si può immergere in prima persone nelle prove.
Link al file Geogebra: numprove
Link al file: attività2
3. la sostanza del teorema
Riassumendo…
Siamo giunti all’enunciato semplificato del teorema limite centrale (TLC): è la nostra seconda formulazione, dopo quella ancor più ridotta presentata all’inizio del percorso. Il docente (e anche lo studente) deve esser consapevole del fatto che l’enunciato proposto non è preciso, ma d’altra parte è proprio in tale versione che il teorema trova concretamente applicazione in molti problemi di calcolo.

Link al file: teorema
4. applicazioni: finalmente i sondaggi
Riassumendo…
A questo punto del percorso, disponiamo di tutti gli elementi per risolvere il problema relativo ai sondaggi in modo meno dispendioso computazionalmente. Possiamo così concludere la risoluzione del problema guida. Esso è già stato modellizzato all’inizio del percorso, pertanto si tratta di calcolare effettivamente la probabilità relativa al numero di individui che voteranno uno dei due candidati. Il procedimento che conduce alla risposta è una sintesi dell’intero percorso.
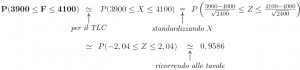
Link al file: ris.sondaggi
5. applicazioni: dall’esame di stato
Riassumendo…
Questo quesito (proposto ben tre volte dal MIUR) si può risolvere sfruttando il modello binomiale, ma la seconda richiesta comporta calcoli dispendiosi, anche se non esplicitamente richiesti nel testo. E’ qui allora che l’uso del TLC acquista valore, permettendo di risolvere l’esercizio in modo più efficace.

Link al file: quesito
|
DOWNLOAD |
