| Modalità d’uso per il docente
Appurata la loro significatività, esaminiamo ora la famiglia di funzioni il cui grafico è la curva “a campana” e decidiamo di farlo ivestigando prima sulle loro caratteristiche analitiche. Il materiale proposto in questa sezione è strutturato nella forma di attività guidata: alla richiesta fanno seguito i suggerimenti, le indicazioni per l’uso del file Geogebra dove presente e infine la risoluzione. In questo modo lo studente può lavorare autonomamente, anche a casa. |
1. prime esplorazioni -attivita’-
Riassumendo…
L’attività richiede agli studenti di disegnare alcuni grafici della famiglia di funzioni in esame. Il lavoro è arricchito dalla possibilità di utilizzare un file Geogebra che permette di visualizzare i grafici delle funzioni considerate.

Link al file Geogebra: curvacampana
Link al file: esplorazioni
2. caratteristiche analitiche delle funzioni -attivita’-
Riassumendo…
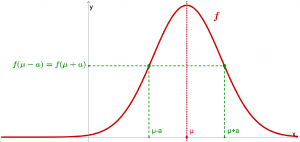
Mediante questa attività vogliamo scoprire (e giustificare) alcune proprietà della famiglia di funzioni f. Tra le possibili, abbiamo scelto di analizzare quelle di cui lo studente dovrebbe disporre in modo immediato lungo tutto il percorso: simmetrie del grafico, punto di massimo e punti di flesso.

Link al file: caratt_analitiche
3. significato geometrico dei parametri -attivita’-
Riassumendo…
L’attività è improntata all’investigazione del significato geometrico dei parametri μ e σ della famiglia di funzioni. Per attuare l’esplorazione, gli studenti hanno a disposizione un file Geogebra che viene qui usato non come semplice strumento di controllo, ma come supporto essenziale per condurre l’attività. Il software Geogebra si presta bene a questo compito, in quanto, mediante l’uso degli slider, permette di visualizzare in modo dinamico come cambiano i grafici al variare dei parametri.

Link al file Geogebra: parametri
Link al file: parametri
|
DOWNLOAD Una famiglia di funzioni: aspetti analitici – il punto di vista del docente Una famiglia di funzioni: aspetti analitici – materiali per gli studenti |
