| Modalità d’uso per il docente
I materiali creati a supporto di questa prima sezione del percorso sono dispense; esse costituiscono un riferimento per condurre una lezione partecipata. Ulteriori approfondimenti possono essere condotti sfruttando il link al sito ministeriale www.sondaggipoliticoelettorali.it, che raccoglie i sondaggi, oppure con letture mirate che trattano altre situazioni in cui compare la curva “a campana”. |
1. I SONDAGGI
Riassumendo…
I sondaggi sono la situazione motivante con cui abbiamo scelto di introdurre il percorso sulla distribuzione normale. In particolare facciamo osservare agli studenti che l’importanza dei sondaggi è stabilita per legge, non è solo una questione matematica, dato che essi devono essere riportati su un sito gestito dallo Stato. Dopo aver fatto una breve analisi di un sondaggio, illustrando il significato dei termini e dei dati presenti, conviene focalizzare l’attenzione su un quesito specifico. Esso costituirà il nostro problema guida per l’intero percorso.

Link al file: sondaggi
2. un modello binomiale
Riassumendo…
Proviamo a modellizzare la situazione proposta mediante la distribuzione binomiale. Il calcolo finale a cui si giunge è assai articolato per la presenza dei coefficienti binomiali, pertanto siamo interessati a trovare un modo più efficace per risolvere il problema. Ciò consente di radicare con continuità i saperi nuovi sui progressi: se non si forniscono agli studenti le occasioni per prendere consapevolezza dei limiti delle procedure di cui dispongono, essi difficilmente potranno cogliere la necessità e il ruolo degli oggetti che si introducono.
Link al file: binomiale
3. un nuovo modello: verso il tlc
Riassumendo…
Attraverso un approccio grafico, viene discussa l’idea di approssimare la distribuzione binomiale mediante un nuovo modello e si precisa tale approssimazione in una prima elementare formulazione del teorema limite centrale. Ciò permette di esprimere il problema guida in una nuova forma che prevede il ricorso alla curva “a campana” e, come si vedrà, comporta una notevole semplificazione computazionale.
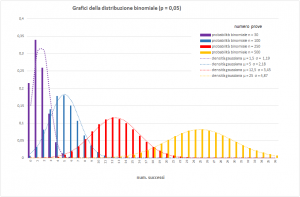
Link al file: versoTLC
4. altre motivazioni alla normale
Riassumendo…
La curva “a campana” compare in molti altri contesti. Tra questi ci sono due situazioni significative dal punto di vista dello sviluppo storico che pertanto proponiamo agli studenti: la distribuzione degli errori accidentali nella misura e la legge delle altezze di una popolazione.
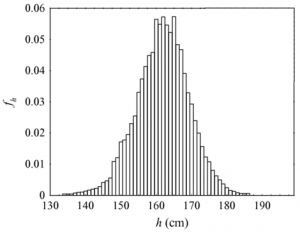
Link al file: motivazioni
5. facciamo il punto
Riassumendo…
Al termine di questo segmento, discutiamo le conclusioni: gli studenti dovrebbero essere ormai convinti dell’importanza di studiare la curva normale, che hanno visto intervenire in contesti così diversi. Ora ne presentiamo l’espressione analitica, che descriviamo come famiglia di funzioni al variare dei parametri reali μ e σ.

Link al file: ilpunto
|
DOWNLOAD |
